Fundamental Data Structures In JavaScript
Fundamental Data Structures In JavaScript
Data structures in JavaScript
Here's a website I created to practice data structures! directory Edit descriptionds-algo-official-c3dw6uapg-bgoonz.vercel.app
Here's the repo that the website is built on: bgoonz/DS-ALGO-OFFICIAL Navigation ####Author:Bryan Guner Big O notation is the language we use for talking about how long an algorithm takes…github.com
Resources (article content below):
Videos
- Data structures by mycodeschoolPre-requisite for this lesson is good understanding of pointers in C.
Books
- Introduction to Algorithms by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein
- Competitive Programming 3 by Steven Halim and Felix Halim
- Competitive Programmers Hand Book Beginner friendly hand book for competitive programmers.
- Data Structures and Algorithms Made Easy by Narasimha Karumanchi
- Learning Algorithms Through Programming and Puzzle Solving by Alexander Kulikov and Pavel Pevzner
Coding practice
- LeetCode
- InterviewBit
- Codility
- HackerRank
- Project Euler
- Spoj
- Google Code Jam practice problems
- HackerEarth
- Top Coder
- CodeChef
- Codewars
- CodeSignal
- CodeKata
- Firecode
Courses
- Master the Coding Interview: Big Tech (FAANG) Interviews Course by Andrei and his team.
- Common Python Data Structures Data structures are the fundamental constructs around which you build your programs. Each data structure provides a particular way of organizing data so it can be accessed efficiently, depending on your use case. Python ships with an extensive set of data structures in its standard library.
- Fork CPP A good course for beginners.
- EDU Advanced course.
- C++ For Programmers Learn features and constructs for C++.
Guides
- GeeksForGeeks — A CS portal for geeks
- Learneroo — Algorithms
- Top Coder tutorials
- Infoarena training path (RO)
- Steven & Felix Halim — Increasing the Lower Bound of Programming Contests (UVA Online Judge)
space
The space complexity represents the memory consumption of a data structure. As for most of the things in life, you can't have it all, so it is with the data structures. You will generally need to trade some time for space or the other way around.
time
The time complexity for a data structure is in general more diverse than its space complexity.
Several operations
In contrary to algorithms, when you look at the time complexity for data structures you need to express it for several operations that you can do with data structures. It can be adding elements, deleting elements, accessing an element or even searching for an element.
Dependent on data
Something that data structure and algorithms have in common when talking about time complexity is that they are both dealing with data. When you deal with data you become dependent on them and as a result the time complexity is also dependent of the data that you received. To solve this problem we talk about 3 different time complexity.
- The best-case complexity: when the data looks the best
- The worst-case complexity: when the data looks the worst
- The average-case complexity: when the data looks average
Big O notation
The complexity is usually expressed with the Big O notation. The wikipedia page about this subject is pretty complex but you can find here a good summary of the different complexity for the most famous data structures and sorting algorithms.
The Array data structure
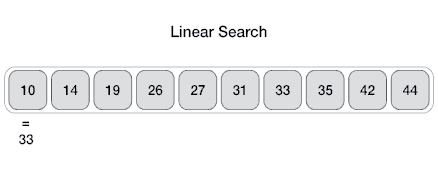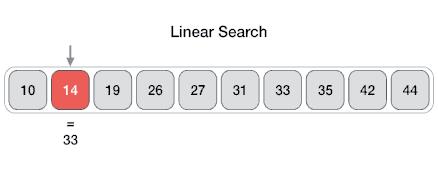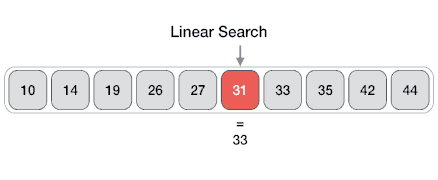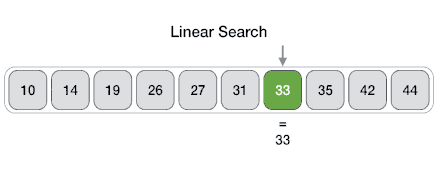
Definition
An Array data structure, or simply an Array, is a data structure consisting of a collection of elements (values or variables), each identified by at least one array index or key. The simplest type of data structure is a linear array, also called one-dimensional array. From Wikipedia
Arrays are among the oldest and most important data structures and are used by every program. They are also used to implement many other data structures.
ComplexityAverageAccess Search Insertion Deletion
O(1) O(n) O(1) O(n)
class ArrayADT {
constructor() {
this.array = [];
}
add(data) {
this.array.push(data);
}
remove(data) {
this.array = this.array.filter((current) => current !== data);
}
search(data) {
const foundIndex = this.array.indexOf(data);
if (foundIndex === -1) {
return foundIndex;
}
return null;
}
getAtIndex(index) {
return this.array[index];
}
length() {
return this.array.length;
}
print() {
console.log(this.array.join(' '));
}
}
const array = new ArrayADT();
console.log('const array = new ArrayADT();: ', array);
console.log('-------------------------------');
console.log('array.add(1): ', array.add(1));
array.add(3);
array.add(4);
console.log('array.add(2);: ', array.add(2), 'array.add(3);', array.add(3), 'array.add(4); ', array.add(4));
console.log('-------------------------------');
array.print();
console.log('-------------------------------');
console.log('search 3 gives index 2:', array.search(3));
console.log('-------------------------------');
console.log('getAtIndex 2 gives 3:', array.getAtIndex(2));
console.log('-------------------------------');
console.log('length is 4:', array.length());
console.log('-------------------------------');
array.remove(3);
array.print();
console.log('-------------------------------');
array.add(5);
array.add(5);
array.print();
console.log('-------------------------------');
array.remove(5);
array.print();
console.log('-------------------------------');
/*
~ final : (master) node 01-array.js
const array = new ArrayADT();: ArrayADT { array: [] }
-------------------------------
array.add(1): undefined
array.add(2);: undefined array.add(3); undefined array.add(4); undefined
-------------------------------
1 3 4 2 3 4
-------------------------------
search 3 gives index 2: null
-------------------------------
getAtIndex 2 gives 3: 4
-------------------------------
length is 4: 6
-------------------------------
1 4 2 4
-------------------------------
1 4 2 4 5 5
-------------------------------
1 4 2 4
-------------------------------
~ final : (master)
*/

indexvalue0 … this is the first value, stored at zero position
- The index of an array runs in sequence
- This could be useful for storing data that are required to be ordered, such as rankings or queues
- In JavaScript, array's value could be mixed; meaning value of each index could be of different data, be it String, Number or even Objects
// 1. Creating Arrays
let firstArray = ["a","b","c"];
let secondArray = ["d","e","f"];
// 2. Access an Array Item
console.log(firstArray[0]); // Results: "a"
// 3. Loop over an Array
firstArray.forEach(function(item, index, array){
console.log(item, index);
});
// Results:
// a 0
// b 1
// c 2
// 4. Add new item to END of array
secondArray.push('g');
console.log(secondArray);
// Results: ["d","e","f", "g"]
// 5. Remove item from END of array
secondArray.pop();
console.log(secondArray);
// Results: ["d","e","f"]
// 6. Remove item from FRONT of array
secondArray.shift();
console.log(secondArray);
// Results: ["e","f"]
// 7. Add item to FRONT of array
secondArray.unshift("d");
console.log(secondArray);
// Results: ["d","e","f"]
// 8. Find INDEX of an item in array
let position = secondArray.indexOf('f');
// Results: 2
// 9. Remove Item by Index Position
secondArray.splice(position, 1);
console.log(secondArray);
// Note, the second argument, in this case "1",
// represent the number of array elements to be removed
// Results: ["d","e"]
// 10. Copy an Array
let shallowCopy = secondArray.slice();
console.log(secondArray);
console.log(shallowCopy);
// Results: ShallowCopy === ["d","e"]
// 11. JavaScript properties that BEGIN with a digit MUST be accessed using bracket notation
renderer.3d.setTexture(model, 'character.png'); // a syntax error
renderer['3d'].setTexture(model, 'character.png'); // works properly
// 12. Combine two Arrays
let thirdArray = firstArray.concat(secondArray);
console.log(thirdArray);
// ["a","b","c", "d", "e"];
// 13. Combine all Array elements into a string
console.log(thirdArray.join()); // Results: a,b,c,d,e
console.log(thirdArray.join('')); // Results: abcde
console.log(thirdArray.join('-')); // Results: a-b-c-d-e
// 14. Reversing an Array (in place, i.e. destructive)
console.log(thirdArray.reverse()); // ["e", "d", "c", "b", "a"]
// 15. sort
let unsortedArray = ["Alphabet", "Zoo", "Products", "Computer Science", "Computer"];
console.log(unsortedArray.sort());
// Results: ["Alphabet", "Computer", "Computer Science", "Products", "Zoo" ]
2. Objects
Think of objects as a logical grouping of a bunch of properties.
Properties could be some variable that it's storing or some methods that it's using.
I also visualize an object as a table.
The main difference is that object's "index" need not be numbers and is not necessarily sequenced.

// 16. Creating an Object
let newObj = {
name: "I'm an object",
values: [1, 10, 11, 20],
others: '',
'1property': 'example of property name starting with digit'
};
// 17. Figure out what keys/properties are in an object
console.log(Object.keys(newObj));
// Results: [ 'name', 'values', 'others', '1property' ]
// 18. Show all values stored in the object
console.log(Object.values(newObj));
// Results:
// [ 'I\'m an object',
// [ 1, 10, 11, 20 ],
// '',
// 'example of property name starting with digit' ]
// 19. Show all key and values of the object
for (let [key, value] of Object.entries(newObj)) {
console.log(`${key}: ${value}`);
}
// Results:
// name: I'm an object
// values: 1,10,11,20
// others:
// 1property: example of property name starting with digit
// 20. Accessing Object's Properties
// Two different ways to access properties, both produce same results
console.log(newObj.name);
console.log(newObj['name']);
// But if the property name starts with a digit,
// we CANNOT use dot notation
console.log(newObj['1property']);
// 21. Adding a Method to an Object
newObj.helloWorld = function () {
console.log('Hello World from inside an object!');
};
// 22. Invoking an Object's Method
newObj.helloWorld();
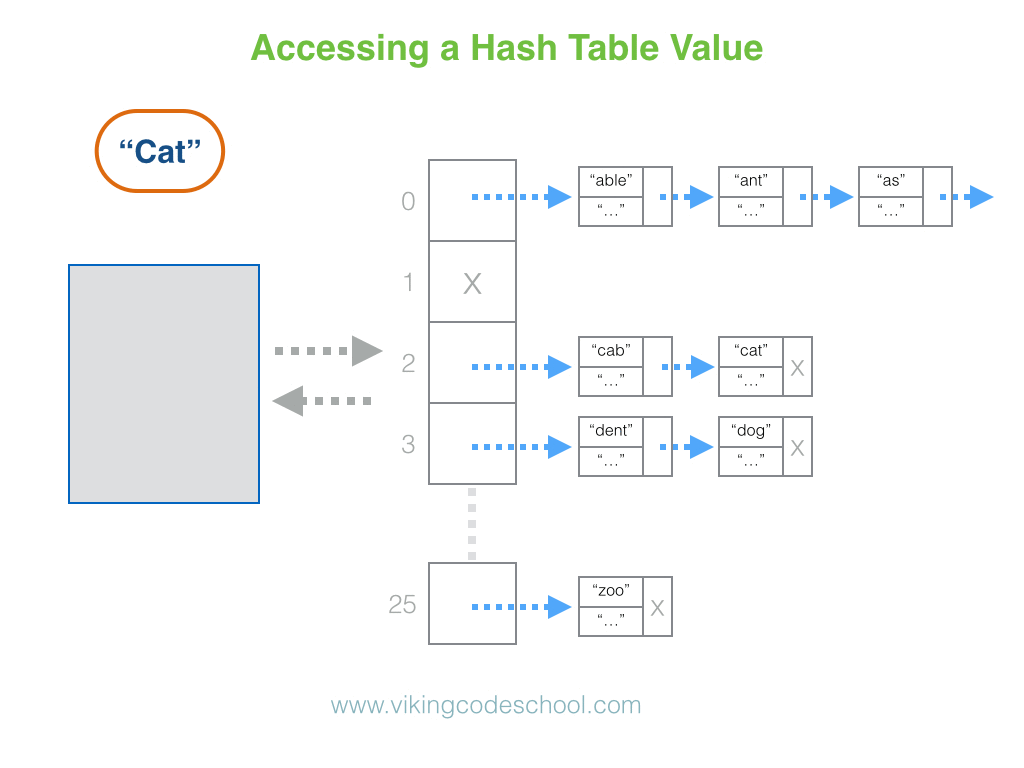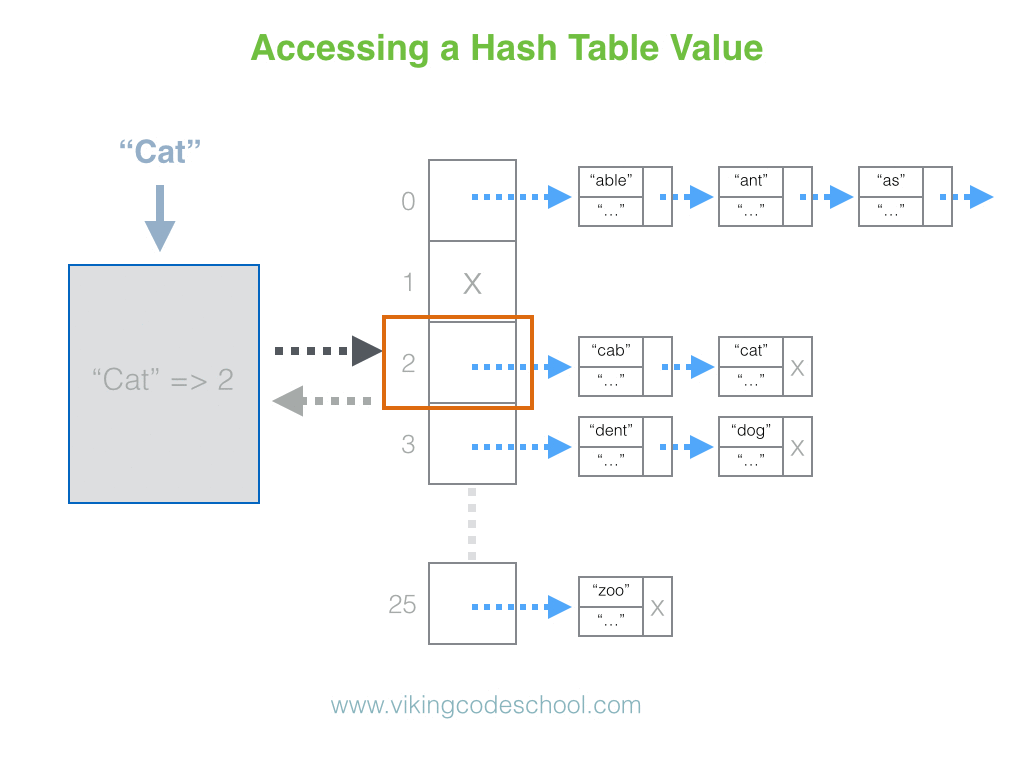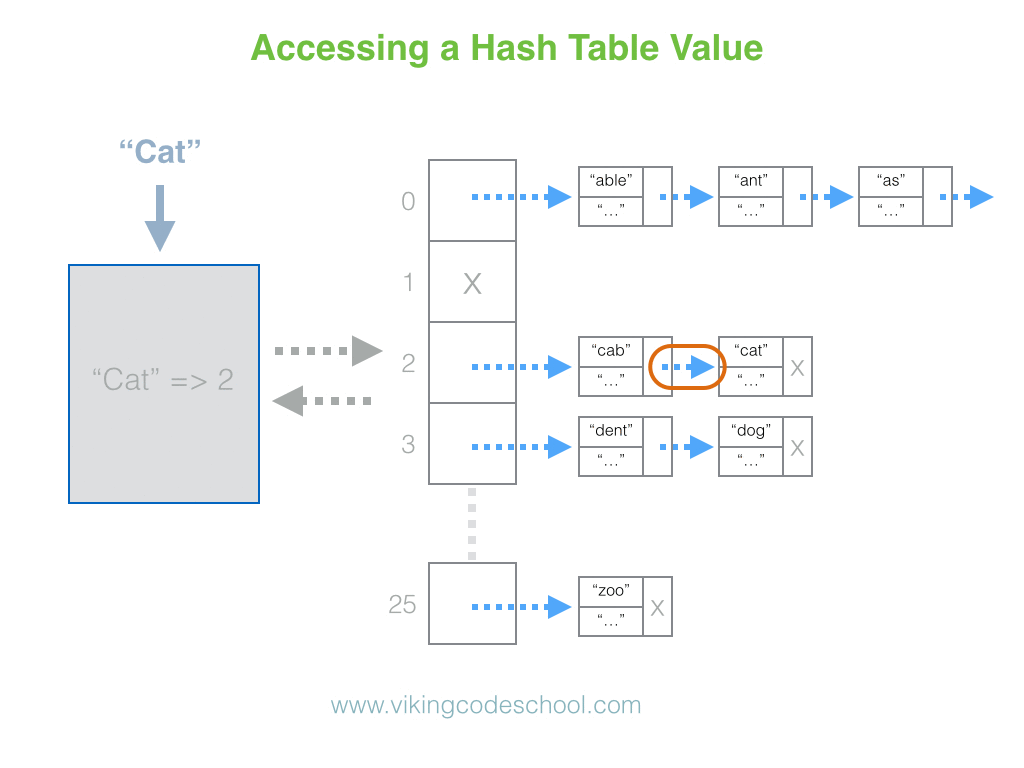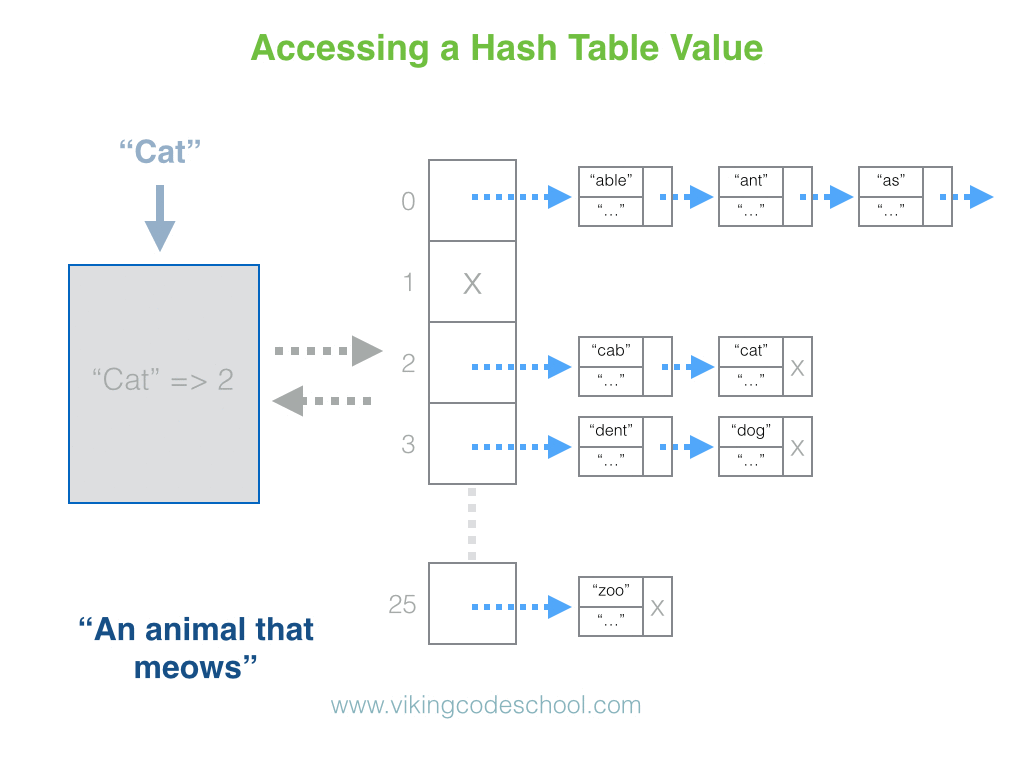
The Hash Table

Definition
A Hash Table (Hash Map) is a data structure used to implement an associative array, a structure that can map keys to values. A Hash Table uses a hash function to compute an index into an array of buckets or slots, from which the desired value can be found. From Wikipedia
Hash Tables are considered the more efficient data structure for lookup and for this reason, they are widely used.
Complexity Average Access Search Insertion Deletion
O(1) O(1) O(1)
The code
Note, here I am storing another object for every hash in my Hash Table.
class HashTable {
constructor(size) {
this.values = {};
this.numberOfValues = 0;
this.size = size;
}
add(key, value) {
let hash = this.calculateHash(key);
if (!this.values.hasOwnProperty(hash)) {
this.values[hash] = {};
}
if (!this.values[hash].hasOwnProperty(key)) {
this.numberOfValues++;
}
this.values[hash][key] = value;
}
remove(key) {
let hash = this.calculateHash(key);
if (this.values.hasOwnProperty(hash) && this.values[hash].hasOwnProperty(key)) {
delete this.values[hash][key];
this.numberOfValues--;
}
}
calculateHash(key) {
return key.toString().length % this.size;
}
search(key) {
let hash = this.calculateHash(key);
if (this.values.hasOwnProperty(hash) && this.values[hash].hasOwnProperty(key)) {
return this.values[hash][key];
} else {
return null;
}
}
length() {
return this.numberOfValues;
}
print() {
let string = '';
for (let value in this.values) {
for (let key in this.values[value]) {
string += this.values[value][key] + ' ';
}
}
console.log(string.trim());
}
}
let hashTable = new HashTable(3);
hashTable.add('first', 1);
hashTable.add('second', 2);
hashTable.add('third', 3);
hashTable.add('fourth', 4);
hashTable.add('fifth', 5);
hashTable.print(); // => 2 4 1 3 5
console.log('length gives 5:', hashTable.length()); // => 5
console.log('search second gives 2:', hashTable.search('second')); // => 2
hashTable.remove('fourth');
hashTable.remove('first');
hashTable.print(); // => 2 3 5
console.log('length gives 3:', hashTable.length()); // => 3
/*
~ js-files : (master) node hash.js
2 4 1 3 5
length gives 5: 5
search second gives 2: 2
2 3 5
length gives 3: 3
*/
The Set
Sets
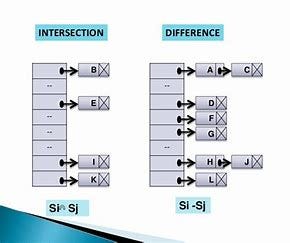
Sets are pretty much what it sounds like. It's the same intuition as Set in Mathematics. I visualize Sets as Venn Diagrams.
// 23. Creating a new Set
let newSet = new Set();
// 24. Adding new elements to a set
newSet.add(1); // Set[1]
newSet.add('text'); // Set[1, "text"]
// 25. Check if element is in set
newSet.has(1); // true
// 24. Check size of set
console.log(newSet.size); // Results: 2
// 26. Delete element from set
newSet.delete(1); // Set["text"]
// 27. Set Operations: isSuperSet
function isSuperset(set, subset) {
for (let elem of subset) {
if (!set.has(elem)) {
return false;
}
}
return true;
}
// 28. Set Operations: union
function union(setA, setB) {
let _union = new Set(setA);
for (let elem of setB) {
_union.add(elem);
}
return _union;
}
// 29. Set Operations: intersection
function intersection(setA, setB) {
let _intersection = new Set();
for (let elem of setB) {
if (setA.has(elem)) {
_intersection.add(elem);
}
}
return _intersection;
}
// 30. Set Operations: symmetricDifference
function symmetricDifference(setA, setB) {
let _difference = new Set(setA);
for (let elem of setB) {
if (_difference.has(elem)) {
_difference.delete(elem);
} else {
_difference.add(elem);
}
}
return _difference;
}
// 31. Set Operations: difference
function difference(setA, setB) {
let _difference = new Set(setA);
for (let elem of setB) {
_difference.delete(elem);
}
return _difference;
}
// Examples
let setA = new Set([1, 2, 3, 4]);
let setB = new Set([2, 3]);
let setC = new Set([3, 4, 5, 6]);
console.log(isSuperset(setA, setB)); // => true
console.log(union(setA, setC)); // => Set [1, 2, 3, 4, 5, 6]
console.log(intersection(setA, setC)); // => Set [3, 4]
console.log(symmetricDifference(setA, setC)); // => Set [1, 2, 5, 6]
console.log(difference(setA, setC)); // => Set [1, 2]
Definition
A Set is an abstract data type that can store certain values, without any particular order, and no repeated values. It is a computer implementation of the mathematical concept of a finite Set. From Wikipedia
The Set data structure is usually used to test whether elements belong to set of values. Rather then only containing elements, Sets are more used to perform operations on multiple values at once with methods such as union, intersect, etc…
Complexity Average Access Search Insertion Deletion
O(n) O(n) O(n)
The code
function Set() {
this.values = [];
this.numberOfValues = 0;
}
Set.prototype.add = function (value) {
if (!~this.values.indexOf(value)) {
this.values.push(value);
this.numberOfValues++;
}
};
Set.prototype.remove = function (value) {
let index = this.values.indexOf(value);
if (~index) {
this.values.splice(index, 1);
this.numberOfValues--;
}
};
Set.prototype.contains = function (value) {
return this.values.indexOf(value) !== -1;
};
Set.prototype.union = function (set) {
let newSet = new Set();
set.values.forEach(function (value) {
newSet.add(value);
});
this.values.forEach(function (value) {
newSet.add(value);
});
return newSet;
};
Set.prototype.intersect = function (set) {
let newSet = new Set();
this.values.forEach(function (value) {
if (set.contains(value)) {
newSet.add(value);
}
});
return newSet;
};
Set.prototype.difference = function (set) {
let newSet = new Set();
this.values.forEach(function (value) {
if (!set.contains(value)) {
newSet.add(value);
}
});
return newSet;
};
Set.prototype.isSubset = function (set) {
return set.values.every(function (value) {
return this.contains(value);
}, this);
};
Set.prototype.length = function () {
return this.numberOfValues;
};
Set.prototype.print = function () {
console.log(this.values.join(' '));
};
let set = new Set();
set.add(1);
set.add(2);
set.add(3);
set.add(4);
set.print(); // => 1 2 3 4
set.remove(3);
set.print(); // => 1 2 4
console.log('contains 4 is true:', set.contains(4)); // => true
console.log('contains 3 is false:', set.contains(3)); // => false
console.log('---');
let set1 = new Set();
set1.add(1);
set1.add(2);
let set2 = new Set();
set2.add(2);
set2.add(3);
let set3 = set2.union(set1);
set3.print(); // => 1 2 3
let set4 = set2.intersect(set1);
set4.print(); // => 2
let set5 = set.difference(set3); // 1 2 4 diff 1 2 3
set5.print(); // => 4
let set6 = set3.difference(set); // 1 2 3 diff 1 2 4
set6.print(); // => 3
console.log('set1 subset of set is true:', set.isSubset(set1)); // => true
console.log('set2 subset of set is false:', set.isSubset(set2)); // => false
console.log('set1 length gives 2:', set1.length()); // => 2
console.log('set3 length gives 3:', set3.length()); // => 3
The Singly Linked List
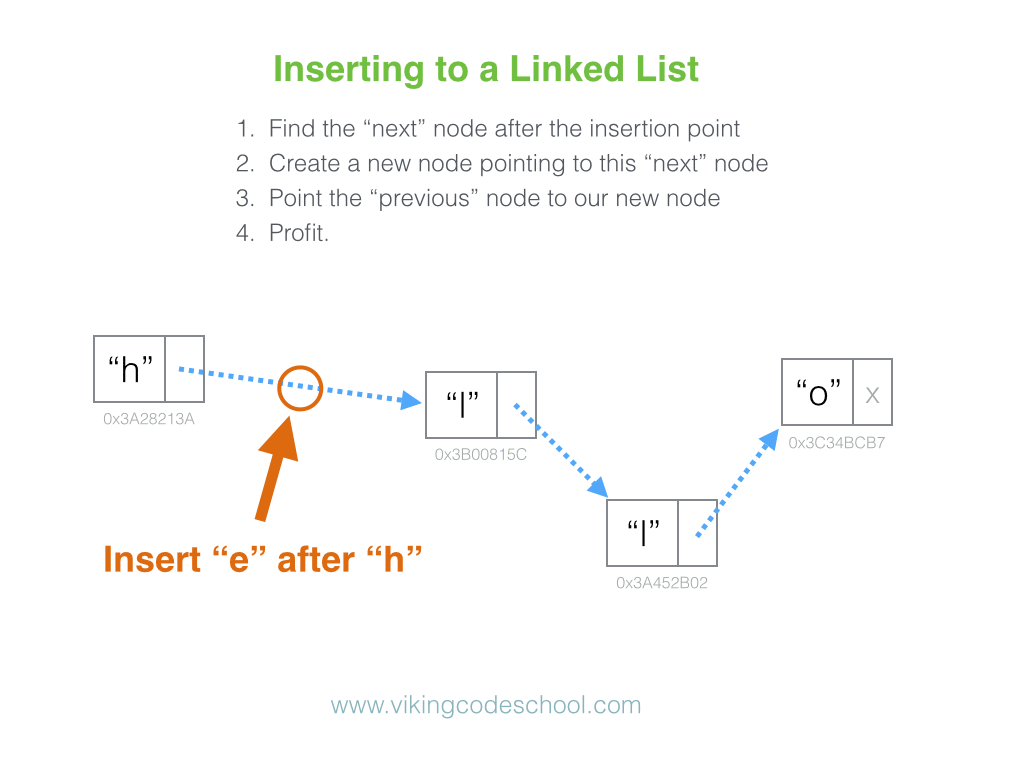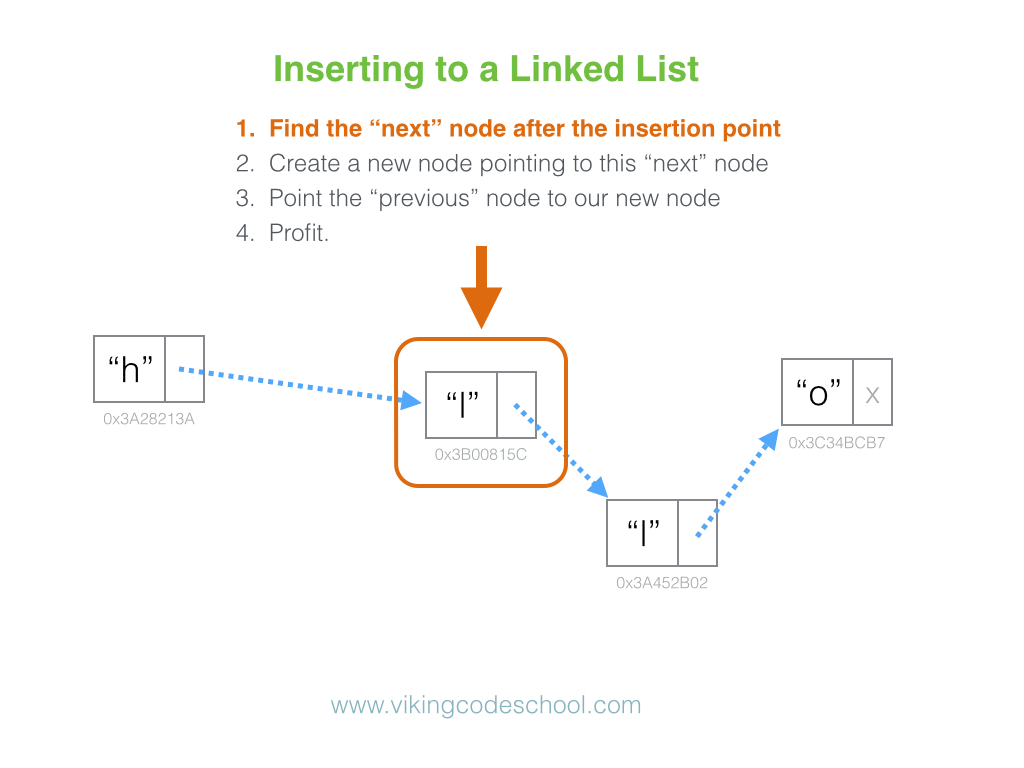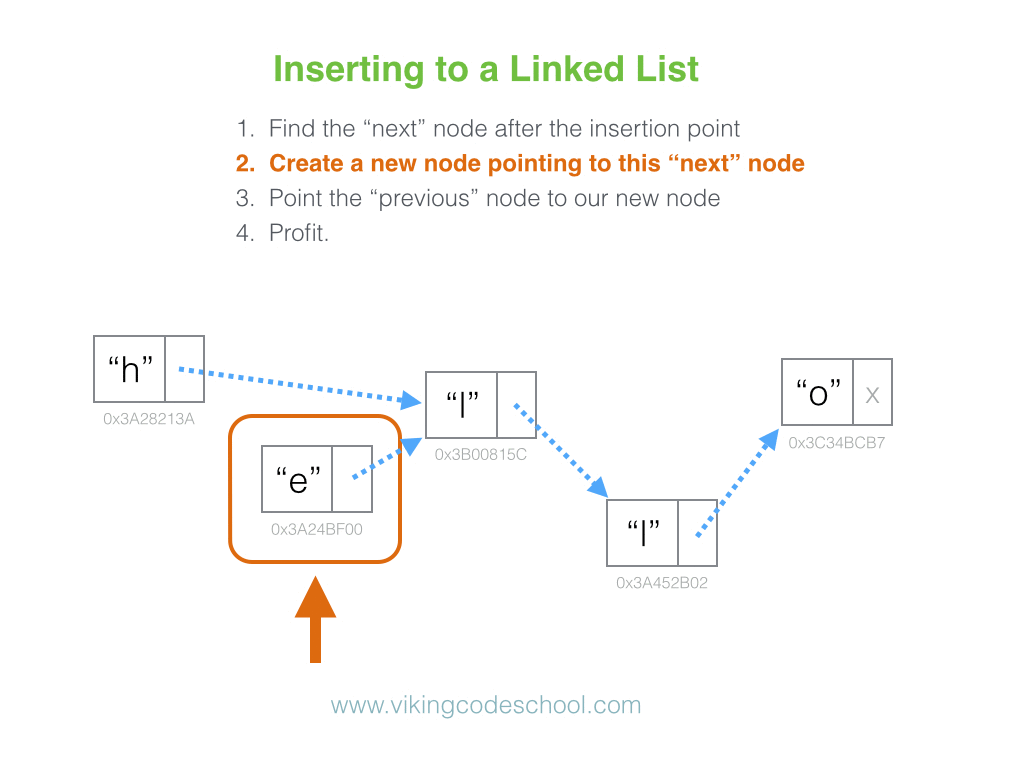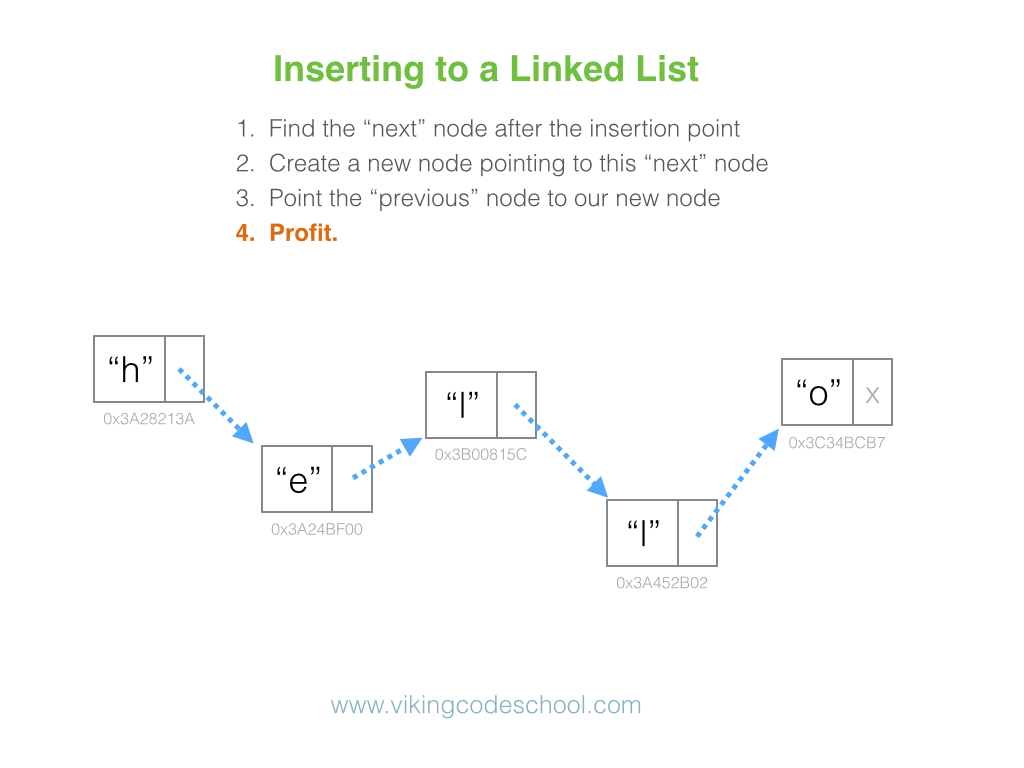
Definition
A Singly Linked List is a linear collection of data elements, called nodes pointing to the next node by means of pointer. It is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of data and a reference (in other words, a link) to the next node in the sequence.
Linked Lists are among the simplest and most common data structures because it allows for efficient insertion or removal of elements from any position in the sequence.
Complexity Average Access Search Insertion Deletion O(n) O(n) O(1) O(1)
The code
function Node(data) {
this.data = data;
this.next = null;
}
function SinglyLinkedList() {
this.head = null;
this.tail = null;
this.numberOfValues = 0;
}
SinglyLinkedList.prototype.add = function (data) {
let node = new Node(data);
if (!this.head) {
this.head = node;
this.tail = node;
} else {
this.tail.next = node;
this.tail = node;
}
this.numberOfValues++;
};
SinglyLinkedList.prototype.remove = function (data) {
let previous = this.head;
let current = this.head;
while (current) {
if (current.data === data) {
if (current === this.head) {
this.head = this.head.next;
}
if (current === this.tail) {
this.tail = previous;
}
previous.next = current.next;
this.numberOfValues--;
} else {
previous = current;
}
current = current.next;
}
};
SinglyLinkedList.prototype.insertAfter = function (data, toNodeData) {
let current = this.head;
while (current) {
if (current.data === toNodeData) {
let node = new Node(data);
if (current === this.tail) {
this.tail.next = node;
this.tail = node;
} else {
node.next = current.next;
current.next = node;
}
this.numberOfValues++;
}
current = current.next;
}
};
SinglyLinkedList.prototype.traverse = function (fn) {
let current = this.head;
while (current) {
if (fn) {
fn(current);
}
current = current.next;
}
};
SinglyLinkedList.prototype.length = function () {
return this.numberOfValues;
};
SinglyLinkedList.prototype.print = function () {
let string = '';
let current = this.head;
while (current) {
string += current.data + ' ';
current = current.next;
}
console.log(string.trim());
};
let singlyLinkedList = new SinglyLinkedList();
singlyLinkedList.print(); // => ''
singlyLinkedList.add(1);
singlyLinkedList.add(2);
singlyLinkedList.add(3);
singlyLinkedList.add(4);
singlyLinkedList.print(); // => 1 2 3 4
console.log('length is 4:', singlyLinkedList.length()); // => 4
singlyLinkedList.remove(3); // remove value
singlyLinkedList.print(); // => 1 2 4
singlyLinkedList.remove(9); // remove non existing value
singlyLinkedList.print(); // => 1 2 4
singlyLinkedList.remove(1); // remove head
singlyLinkedList.print(); // => 2 4
singlyLinkedList.remove(4); // remove tail
singlyLinkedList.print(); // => 2
console.log('length is 1:', singlyLinkedList.length()); // => 1
singlyLinkedList.add(6);
singlyLinkedList.print(); // => 2 6
singlyLinkedList.insertAfter(3, 2);
singlyLinkedList.print(); // => 2 3 6
singlyLinkedList.insertAfter(4, 3);
singlyLinkedList.print(); // => 2 3 4 6
singlyLinkedList.insertAfter(5, 9); // insertAfter a non existing node
singlyLinkedList.print(); // => 2 3 4 6
singlyLinkedList.insertAfter(5, 4);
singlyLinkedList.insertAfter(7, 6); // insertAfter the tail
singlyLinkedList.print(); // => 2 3 4 5 6 7
singlyLinkedList.add(8); // add node with normal method
singlyLinkedList.print(); // => 2 3 4 5 6 7 8
console.log('length is 7:', singlyLinkedList.length()); // => 7
singlyLinkedList.traverse(function (node) {
node.data = node.data + 10;
});
singlyLinkedList.print(); // => 12 13 14 15 16 17 18
singlyLinkedList.traverse(function (node) {
console.log(node.data);
}); // => 12 13 14 15 16 17 18
console.log('length is 7:', singlyLinkedList.length()); // => 7
The Doubly Linked List
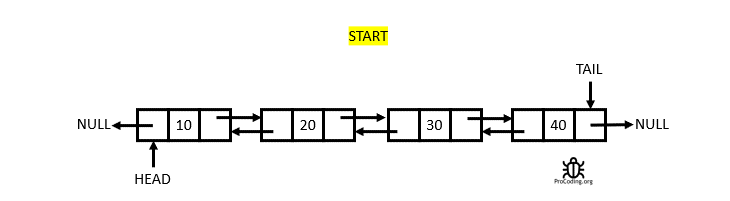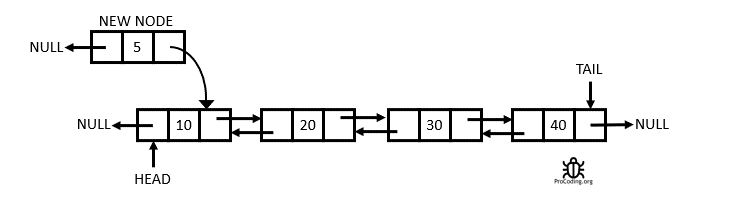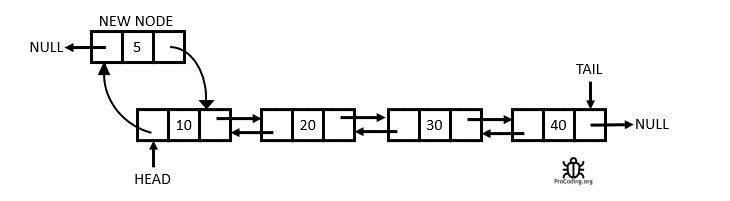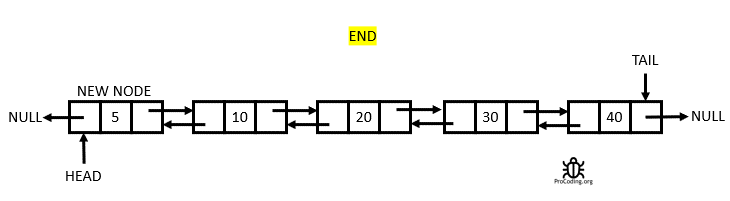
Definition
A Doubly Linked List is a linked data structure that consists of a set of sequentially linked records called nodes. Each node contains two fields, called links, that are references to the previous and to the next node in the sequence of nodes. From Wikipedia
Having two node links allow traversal in either direction but adding or removing a node in a doubly linked list requires changing more links than the same operations on a Singly Linked List.
Complexity Average Access Search Insertion Deletion O(n) O(n) O(1) O(1)
The code
class Node {
constructor(data) {
this.data = data;
this.previous = null;
this.next = null;
}
}
class DoublyLinkedList {
constructor() {
this.head = null;
this.tail = null;
this.numberOfValues = 0;
}
add(data) {
let node = new Node(data);
if (!this.head) {
this.head = node;
this.tail = node;
} else {
node.previous = this.tail;
this.tail.next = node;
this.tail = node;
}
this.numberOfValues++;
}
remove(data) {
let current = this.head;
while (current) {
if (current.data === data) {
if (current === this.head && current === this.tail) {
this.head = null;
this.tail = null;
} else if (current === this.head) {
this.head = this.head.next;
this.head.previous = null;
} else if (current === this.tail) {
this.tail = this.tail.previous;
this.tail.next = null;
} else {
current.previous.next = current.next;
current.next.previous = current.previous;
}
this.numberOfValues--;
}
current = current.next;
}
}
insertAfter(data, toNodeData) {
let current = this.head;
while (current) {
if (current.data === toNodeData) {
let node = new Node(data);
if (current === this.tail) {
this.add(data);
} else {
current.next.previous = node;
node.previous = current;
node.next = current.next;
current.next = node;
this.numberOfValues++;
}
}
current = current.next;
}
}
traverse(fn) {
let current = this.head;
while (current) {
if (fn) {
fn(current);
}
current = current.next;
}
}
traverseReverse(fn) {
let current = this.tail;
while (current) {
if (fn) {
fn(current);
}
current = current.previous;
}
}
length() {
return this.numberOfValues;
}
print() {
let string = "";
let current = this.head;
while (current) {
string += current.data + " ";
current = current.next;
}
console.log(string.trim());
}
}
let doublyLinkedList = new DoublyLinkedList();
doublyLinkedList.print(); // => ''
doublyLinkedList.add(1);
doublyLinkedList.add(2);
doublyLinkedList.add(3);
doublyLinkedList.add(4);
doublyLinkedList.print(); // => 1 2 3 4
console.log("length is 4:", doublyLinkedList.length()); // => 4
doublyLinkedList.remove(3); // remove value
doublyLinkedList.print(); // => 1 2 4
doublyLinkedList.remove(9); // remove non existing value
doublyLinkedList.print(); // => 1 2 4
doublyLinkedList.remove(1); // remove head
doublyLinkedList.print(); // => 2 4
doublyLinkedList.remove(4); // remove tail
doublyLinkedList.print(); // => 2
console.log("length is 1:", doublyLinkedList.length()); // => 1
doublyLinkedList.remove(2); // remove tail, the list should be empty
doublyLinkedList.print(); // => ''
console.log("length is 0:", doublyLinkedList.length()); // => 0
doublyLinkedList.add(2);
doublyLinkedList.add(6);
doublyLinkedList.print(); // => 2 6
doublyLinkedList.insertAfter(3, 2);
doublyLinkedList.print(); // => 2 3 6
doublyLinkedList.traverseReverse(function (node) {
console.log(node.data);
});
doublyLinkedList.insertAfter(4, 3);
doublyLinkedList.print(); // => 2 3 4 6
doublyLinkedList.insertAfter(5, 9); // insertAfter a non existing node
doublyLinkedList.print(); // => 2 3 4 6
doublyLinkedList.insertAfter(5, 4);
doublyLinkedList.insertAfter(7, 6); // insertAfter the tail
doublyLinkedList.print(); // => 2 3 4 5 6 7
doublyLinkedList.add(8); // add node with normal method
doublyLinkedList.print(); // => 2 3 4 5 6 7 8
console.log("length is 7:", doublyLinkedList.length()); // => 7
doublyLinkedList.traverse(function (node) {
node.data = node.data + 10;
});
doublyLinkedList.print(); // => 12 13 14 15 16 17 18
doublyLinkedList.traverse(function (node) {
console.log(node.data);
}); // => 12 13 14 15 16 17 18
console.log("length is 7:", doublyLinkedList.length()); // => 7
doublyLinkedList.traverseReverse(function (node) {
console.log(node.data);
}); // => 18 17 16 15 14 13 12
doublyLinkedList.print(); // => 12 13 14 15 16 17 18
console.log("length is 7:", doublyLinkedList.length()); // => 7
/*
~ js-files : (master) node double-linked-list.js
1 2 3 4
length is 4: 4
1 2 4
1 2 4
2 4
2
length is 1: 1
length is 0: 0
2 6
2 3 6
6
3
2
2 3 4 6
2 3 4 6
2 3 4 5 6 7
2 3 4 5 6 7 8
length is 7: 7
12 13 14 15 16 17 18
12
13
14
15
16
17
18
length is 7: 7
18
17
16
15
14
13
12
12 13 14 15 16 17 18
length is 7: 7
~ js-files : (master)
*/
The Stack
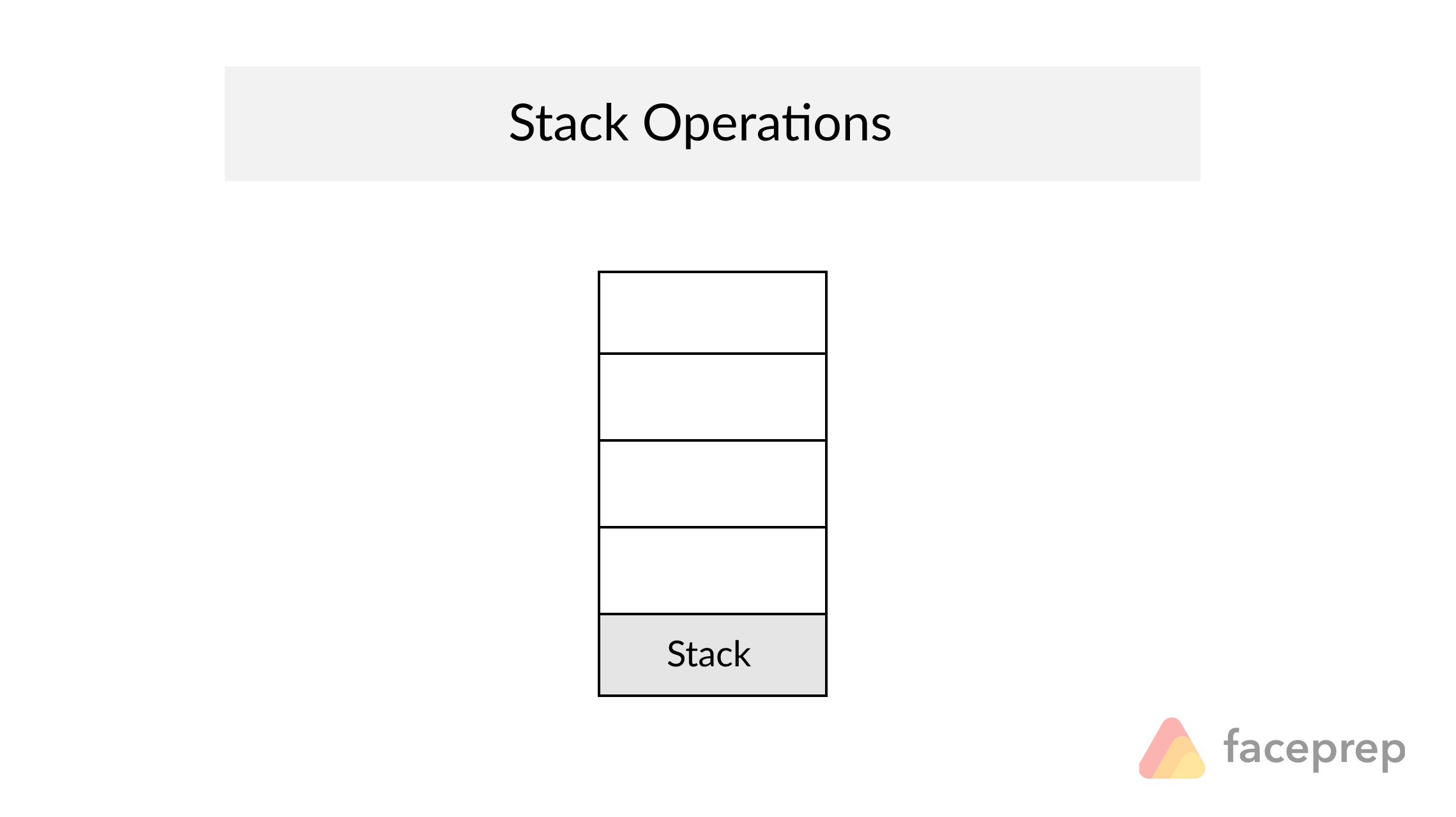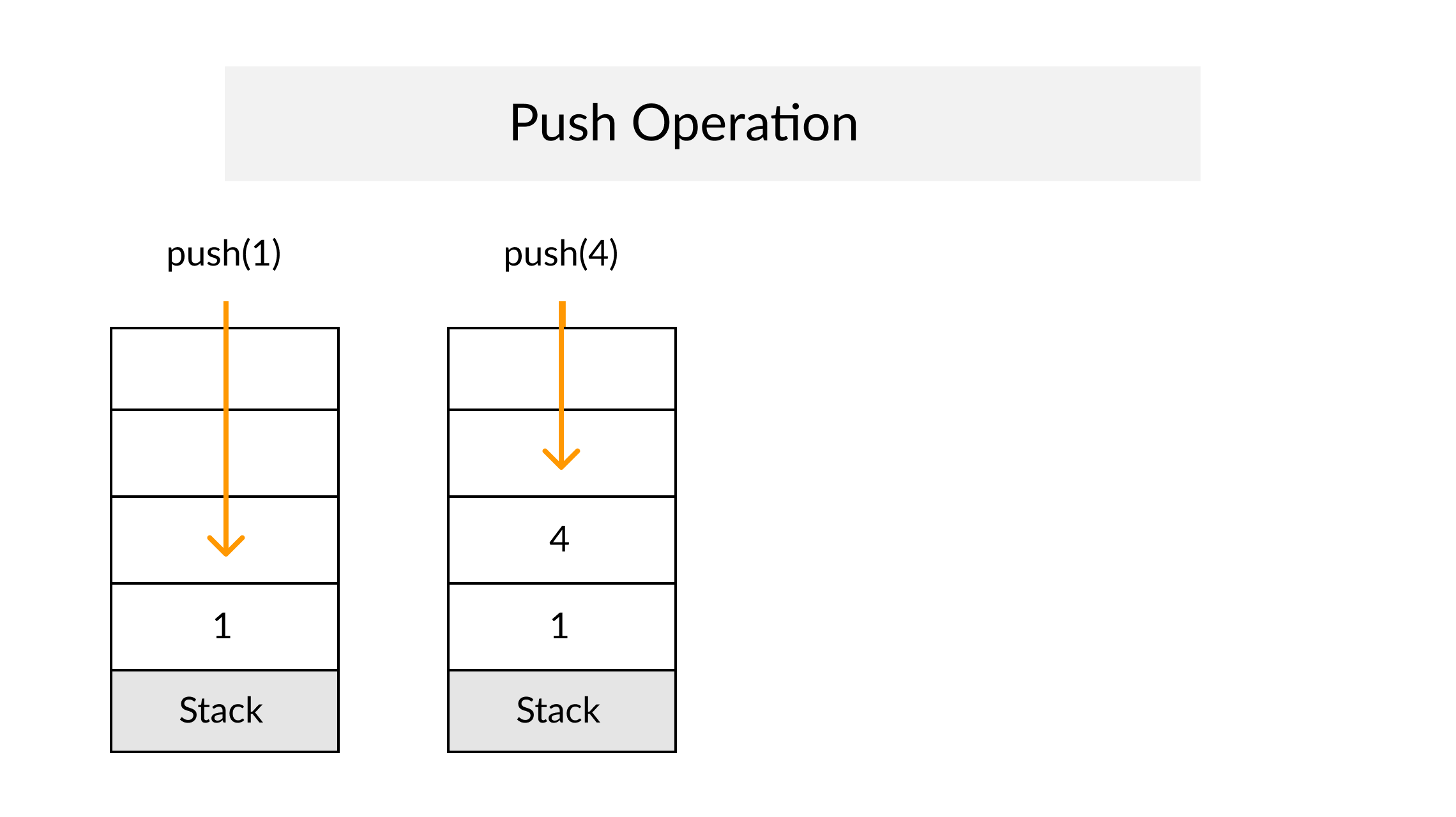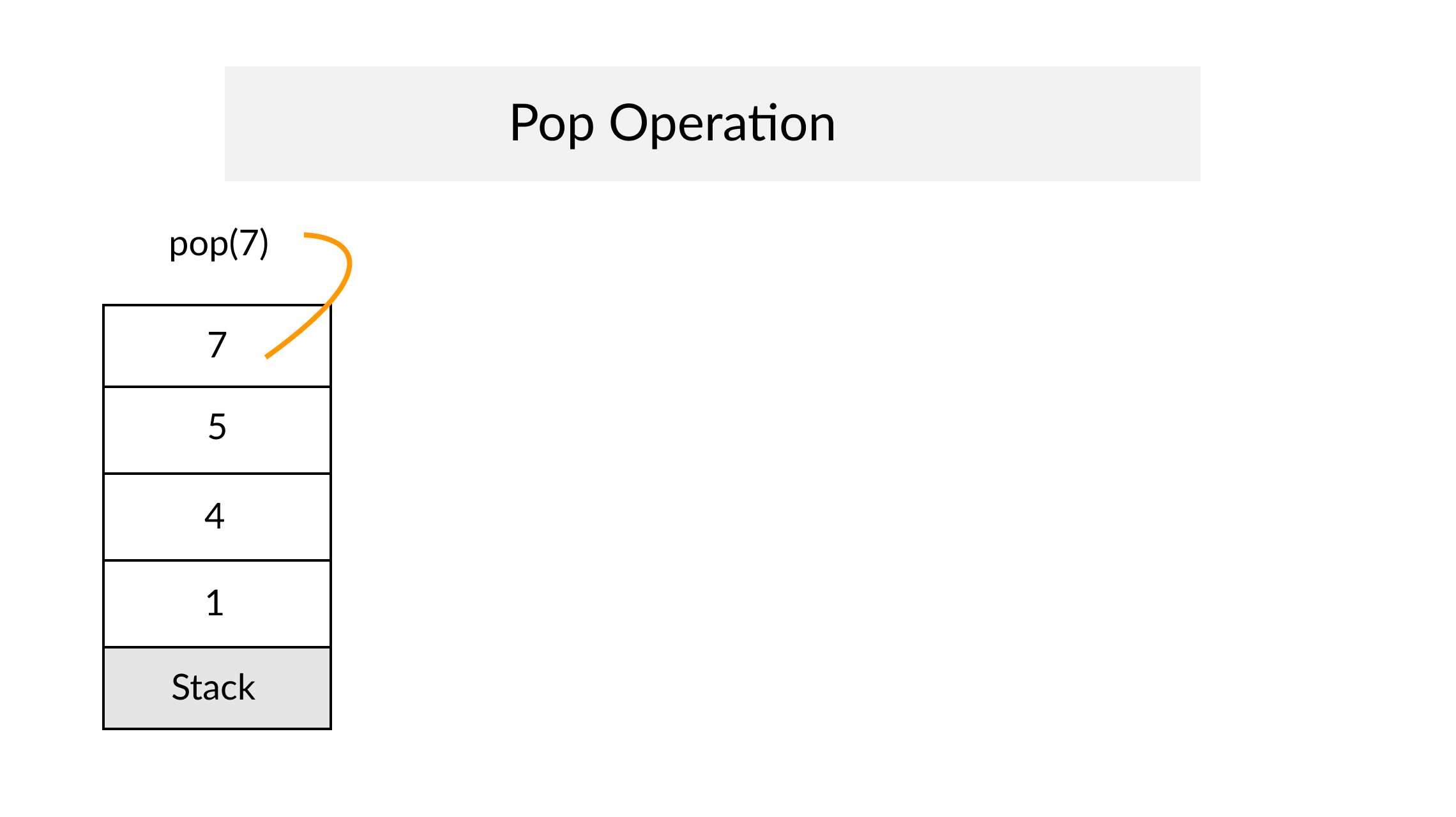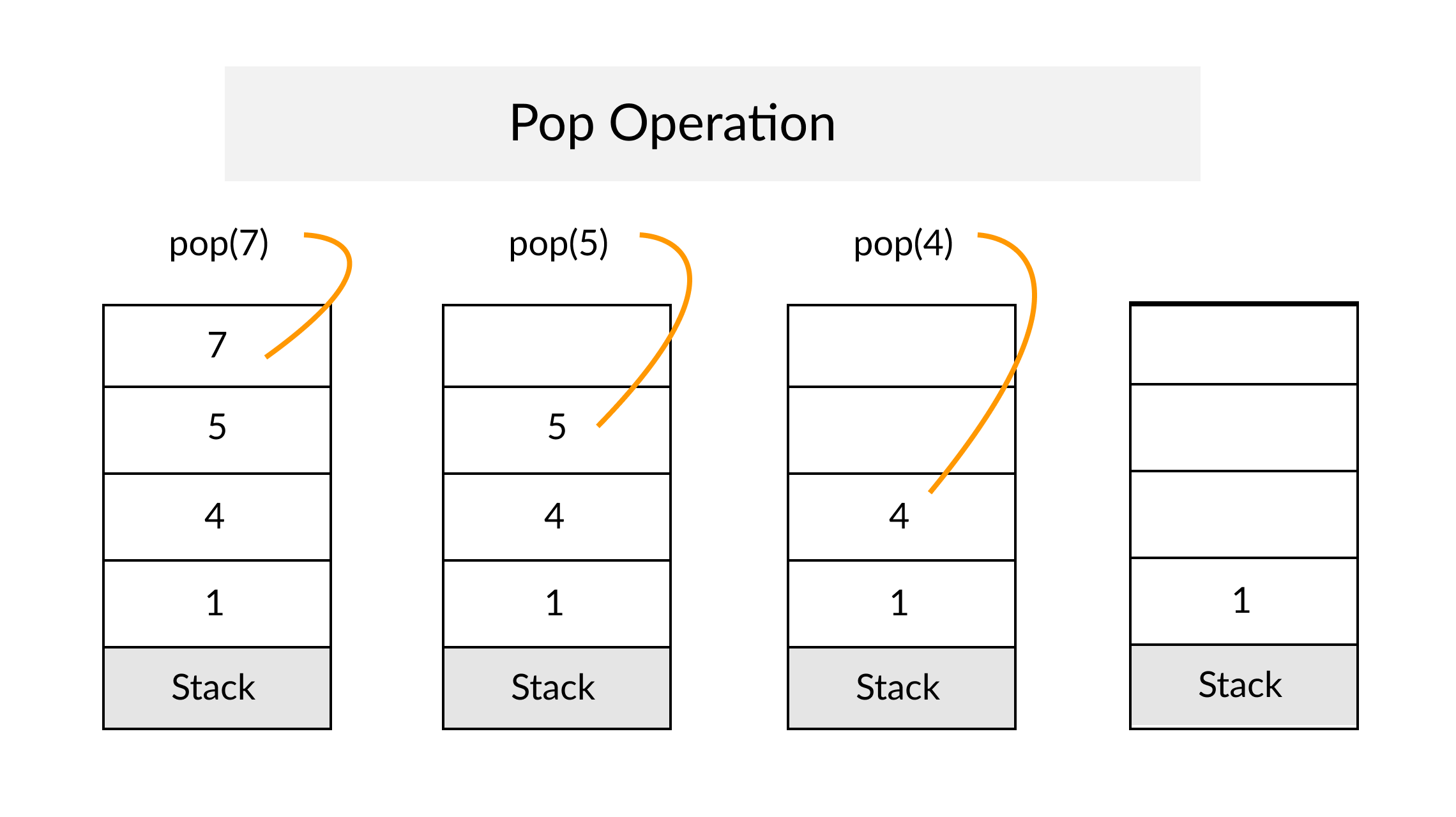
Definition
A Stack is an abstract data type that serves as a collection of elements, with two principal operations: push, which adds an element to the collection, and pop, which removes the most recently added element that was not yet removed. The order in which elements come off a Stack gives rise to its alternative name, LIFO (for last in, first out). From Wikipedia
A Stack often has a third method peek which allows to check the last pushed element without popping it.
Complexity Average Access Search Insertion Deletion O(n) O(n) O(1) O(1)
The code
function Stack() {
this.stack = [];
}
Stack.prototype.push = function(value) {
this.stack.push(value);
};
Stack.prototype.pop = function() {
return this.stack.pop();
};
Stack.prototype.peek = function() {
return this.stack[this.stack.length - 1];
};
Stack.prototype.length = function() {
return this.stack.length;
};
Stack.prototype.print = function() {
console.log(this.stack.join(' '));
};
let stack = new Stack();
stack.push(1);
stack.push(2);
stack.push(3);
stack.print(); // => 1 2 3
console.log('length is 3:', stack.length()); // => 3
console.log('peek is 3:', stack.peek()); // => 3
console.log('pop is 3:', stack.pop()); // => 3
stack.print(); // => 1 2
console.log('pop is 2:', stack.pop()); // => 2
console.log('length is 1:', stack.length()); // => 1
console.log('pop is 1:', stack.pop()); // => 1
stack.print(); // => ''
console.log('peek is undefined:', stack.peek()); // => undefined
console.log('pop is undefined:', stack.pop()); // => undefined
The Queue
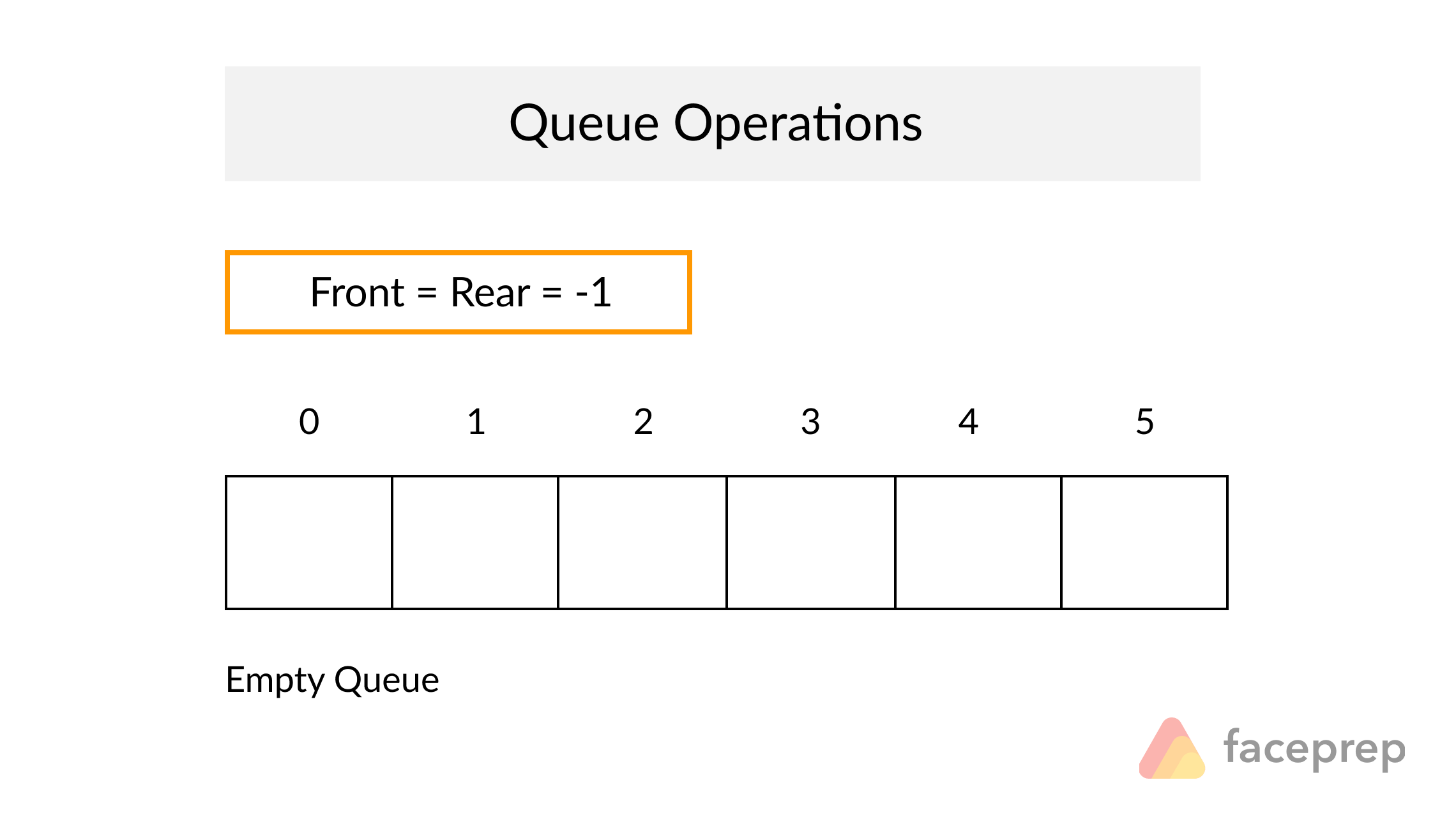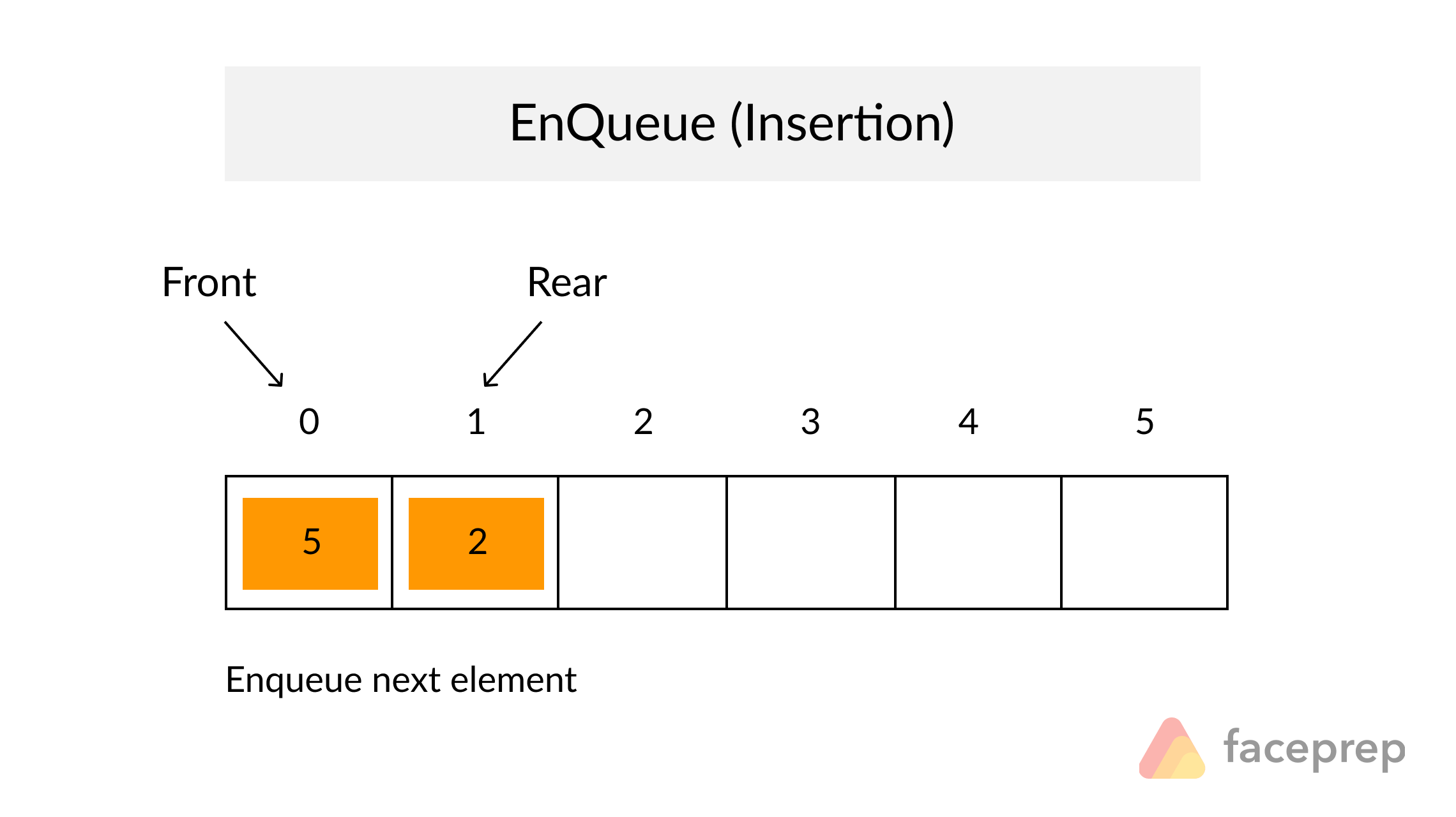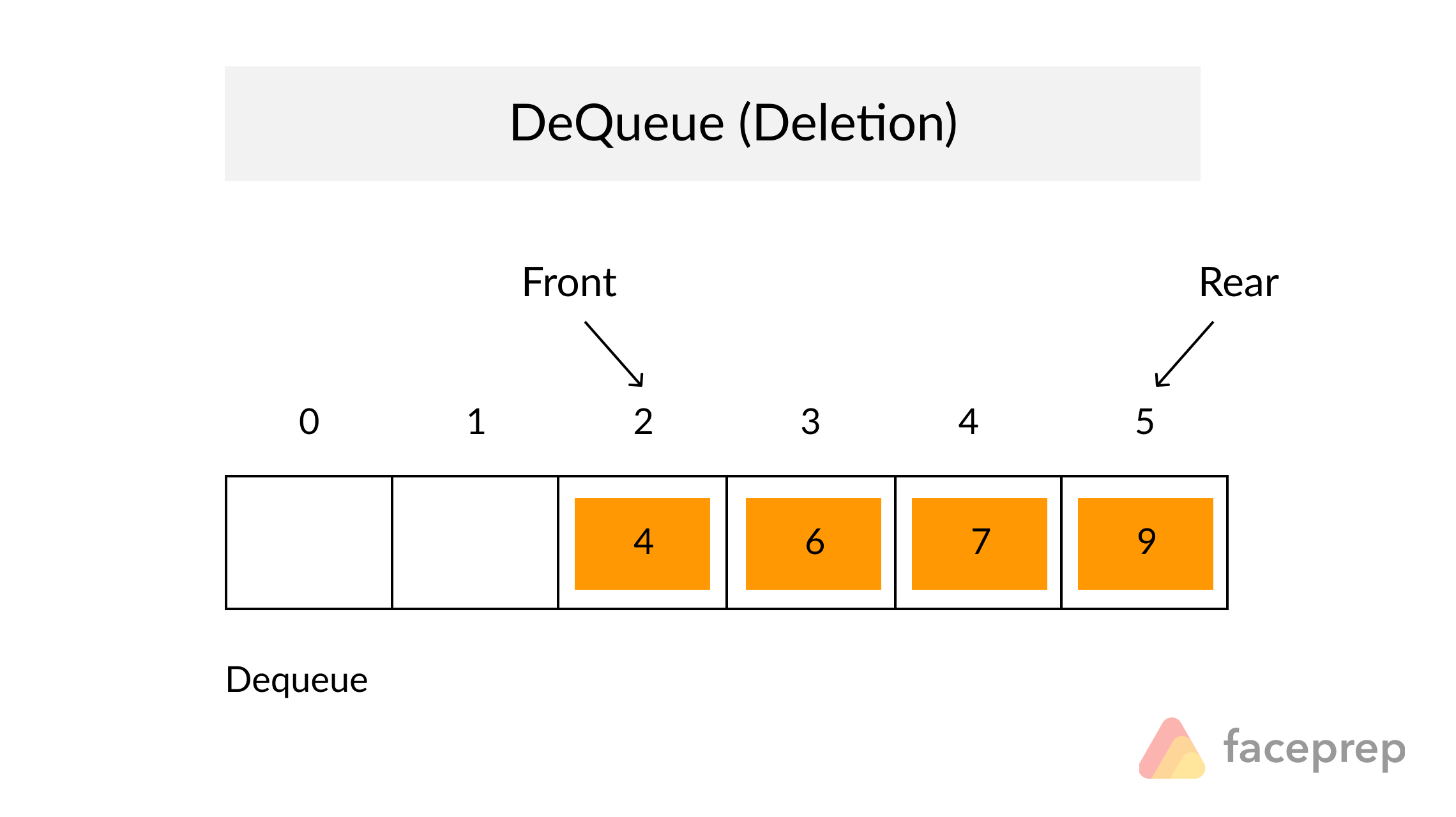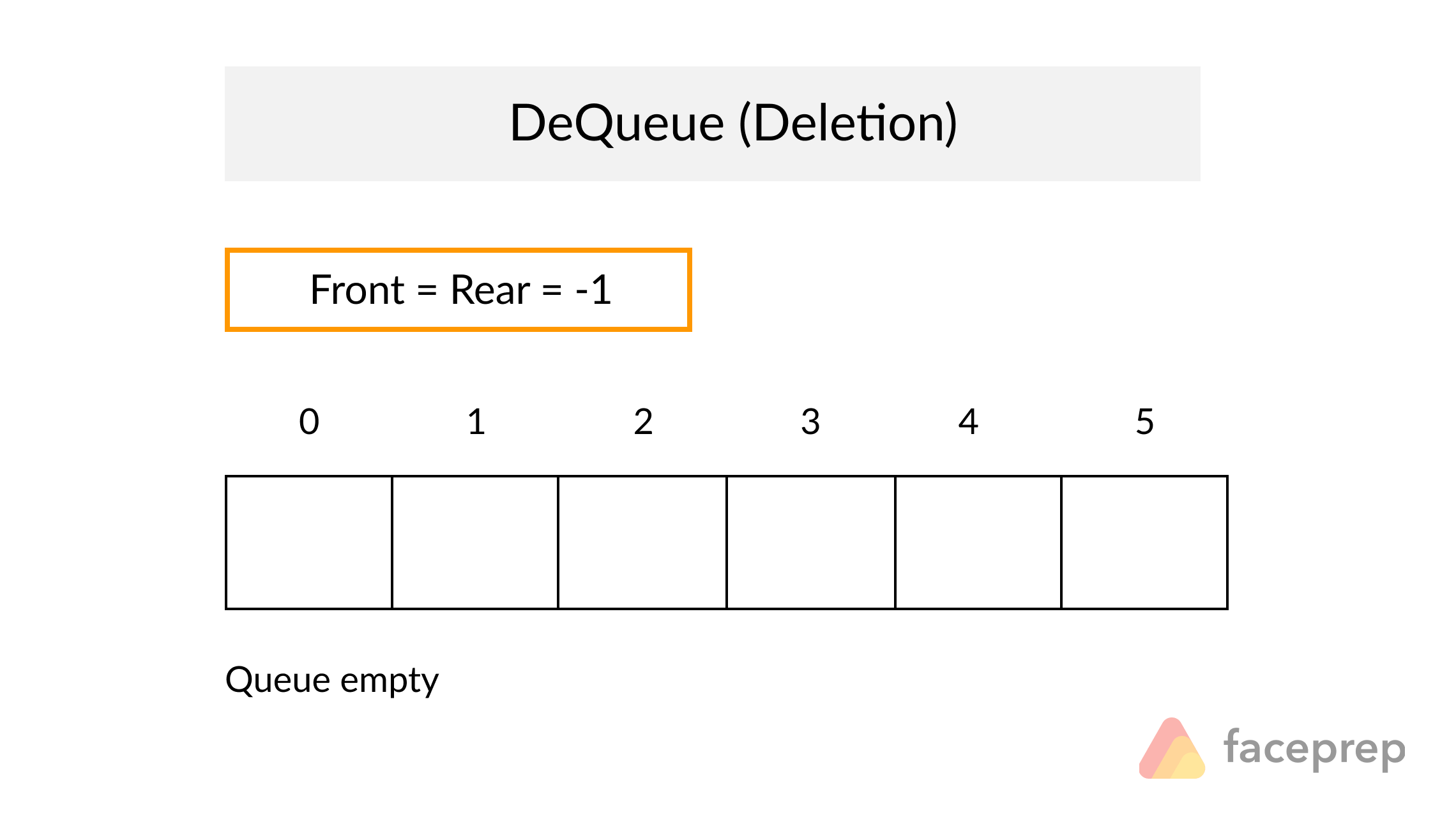
Definition
A Queue is a particular kind of abstract data type or collection in which the entities in the collection are kept in order and the principal operations are the addition of entities to the rear terminal position, known as enqueue, and removal of entities from the front terminal position, known as dequeue. This makes the Queue a First-In-First-Out (FIFO) data structure. In a FIFO data structure, the first element added to the Queue will be the first one to be removed.
As for the Stack data structure, a peek operation is often added to the Queue data structure. It returns the value of the front element without dequeuing it.
Complexity Average Access Search Insertion Deletion O(n) O(n) O(1) O(n)
The code
function Queue() {
this.queue = [];
}
Queue.prototype.enqueue = function(value) {
this.queue.push(value);
};
Queue.prototype.dequeue = function() {
return this.queue.shift();
};
Queue.prototype.peek = function() {
return this.queue[0];
};
Queue.prototype.length = function() {
return this.queue.length;
};
Queue.prototype.print = function() {
console.log(this.queue.join(' '));
};
let queue = new Queue();
queue.enqueue(1);
queue.enqueue(2);
queue.enqueue(3);
queue.print(); // => 1 2 3
console.log('length is 3:', queue.length()); // => 3
console.log('peek is 1:', queue.peek()); // => 3
console.log('dequeue is 1:', queue.dequeue()); // => 1
queue.print(); // => 2 3
console.log('dequeue is 2:', queue.dequeue()); // => 2
console.log('length is 1:', queue.length()); // => 1
console.log('dequeue is 3:', queue.dequeue()); // => 3
queue.print(); // => ''
console.log('peek is undefined:', queue.peek()); // => undefined
console.log('dequeue is undefined:', queue.dequeue()); // => undefined
The Tree
Definition
A Tree is a widely used data structure that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node. A tree data structure can be defined recursively as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root node. From Wikipedia
Complexity Average Access Search Insertion Deletion O(n) O(n) O(n) O(n) To get a full overview of the time and space complexity of the Tree data structure, have a look to this excellent Big O cheat sheet.
The code
function Node(data) {
this.data = data;
this.children = [];
}
function Tree() {
this.root = null;
}
Tree.prototype.add = function(data, toNodeData) {
let node = new Node(data);
let parent = toNodeData ? this.findBFS(toNodeData) : null;
if(parent) {
parent.children.push(node);
} else {
if(!this.root) {
this.root = node;
} else {
return 'Root node is already assigned';
}
}
};
Tree.prototype.remove = function(data) {
if(this.root.data === data) {
this.root = null;
}
let queue = [this.root];
while(queue.length) {
let node = queue.shift();
for(let i = 0; i < node.children.length; i++) {
if(node.children[i].data === data) {
node.children.splice(i, 1);
} else {
queue.push(node.children[i]);
}
}
}
};
Tree.prototype.contains = function(data) {
return this.findBFS(data) ? true : false;
};
Tree.prototype.findBFS = function(data) {
let queue = [this.root];
while(queue.length) {
let node = queue.shift();
if(node.data === data) {
return node;
}
for(let i = 0; i < node.children.length; i++) {
queue.push(node.children[i]);
}
}
return null;
};
Tree.prototype._preOrder = function(node, fn) {
if(node) {
if(fn) {
fn(node);
}
for(let i = 0; i < node.children.length; i++) {
this._preOrder(node.children[i], fn);
}
}
};
Tree.prototype._postOrder = function(node, fn) {
if(node) {
for(let i = 0; i < node.children.length; i++) {
this._postOrder(node.children[i], fn);
}
if(fn) {
fn(node);
}
}
};
Tree.prototype.traverseDFS = function(fn, method) {
let current = this.root;
if(method) {
this['_' + method](current, fn);
} else {
this._preOrder(current, fn);
}
};
Tree.prototype.traverseBFS = function(fn) {
let queue = [this.root];
while(queue.length) {
let node = queue.shift();
if(fn) {
fn(node);
}
for(let i = 0; i < node.children.length; i++) {
queue.push(node.children[i]);
}
}
};
Tree.prototype.print = function() {
if(!this.root) {
return console.log('No root node found');
}
let newline = new Node('|');
let queue = [this.root, newline];
let string = '';
while(queue.length) {
let node = queue.shift();
string += node.data.toString() + ' ';
if(node === newline && queue.length) {
queue.push(newline);
}
for(let i = 0; i < node.children.length; i++) {
queue.push(node.children[i]);
}
}
console.log(string.slice(0, -2).trim());
};
Tree.prototype.printByLevel = function() {
if(!this.root) {
return console.log('No root node found');
}
let newline = new Node('\n');
let queue = [this.root, newline];
let string = '';
while(queue.length) {
let node = queue.shift();
string += node.data.toString() + (node.data !== '\n' ? ' ' : '');
if(node === newline && queue.length) {
queue.push(newline);
}
for(let i = 0; i < node.children.length; i++) {
queue.push(node.children[i]);
}
}
console.log(string.trim());
};
let tree = new Tree();
tree.add('ceo');
tree.add('cto', 'ceo');
tree.add('dev1', 'cto');
tree.add('dev2', 'cto');
tree.add('dev3', 'cto');
tree.add('cfo', 'ceo');
tree.add('accountant', 'cfo');
tree.add('cmo', 'ceo');
tree.print(); // => ceo | cto cfo cmo | dev1 dev2 dev3 accountant
tree.printByLevel(); // => ceo \n cto cfo cmo \n dev1 dev2 dev3 accountant
console.log('tree contains dev1 is true:', tree.contains('dev1')); // => true
console.log('tree contains dev4 is false:', tree.contains('dev4')); // => false
console.log('--- BFS');
tree.traverseBFS(function(node) { console.log(node.data); }); // => ceo cto cfo cmo dev1 dev2 dev3 accountant
console.log('--- DFS preOrder');
tree.traverseDFS(function(node) { console.log(node.data); }, 'preOrder'); // => ceo cto dev1 dev2 dev3 cfo accountant cmo
console.log('--- DFS postOrder');
tree.traverseDFS(function(node) { console.log(node.data); }, 'postOrder'); // => dev1 dev2 dev3 cto accountant cfo cmo ceo
tree.remove('cmo');
tree.print(); // => ceo | cto cfo | dev1 dev2 dev3 accountant
tree.remove('cfo');
tree.print(); // => ceo | cto | dev1 dev2 dev3
The Graph
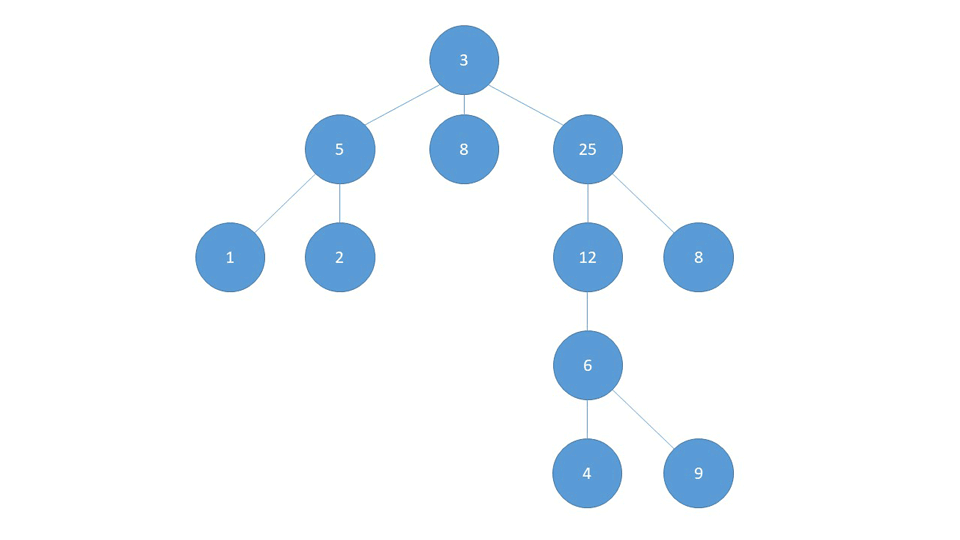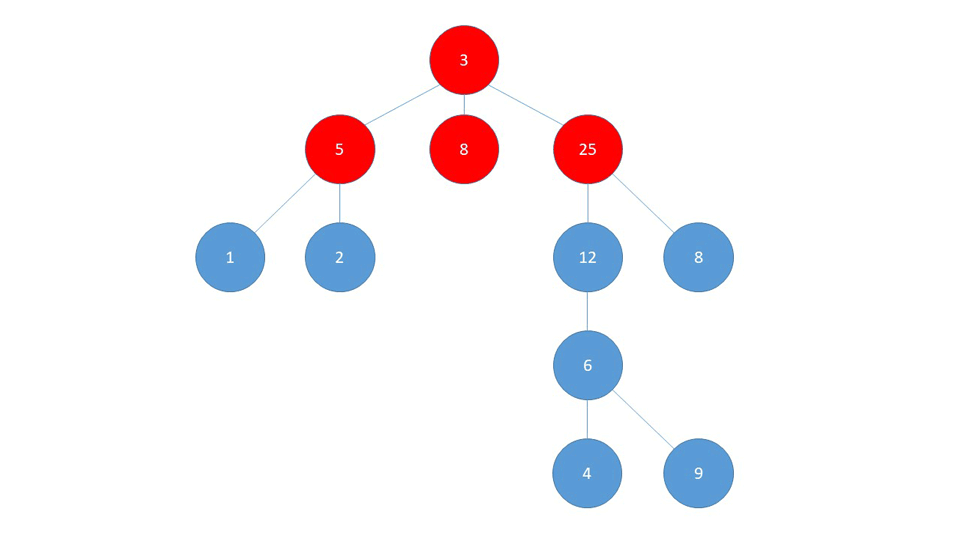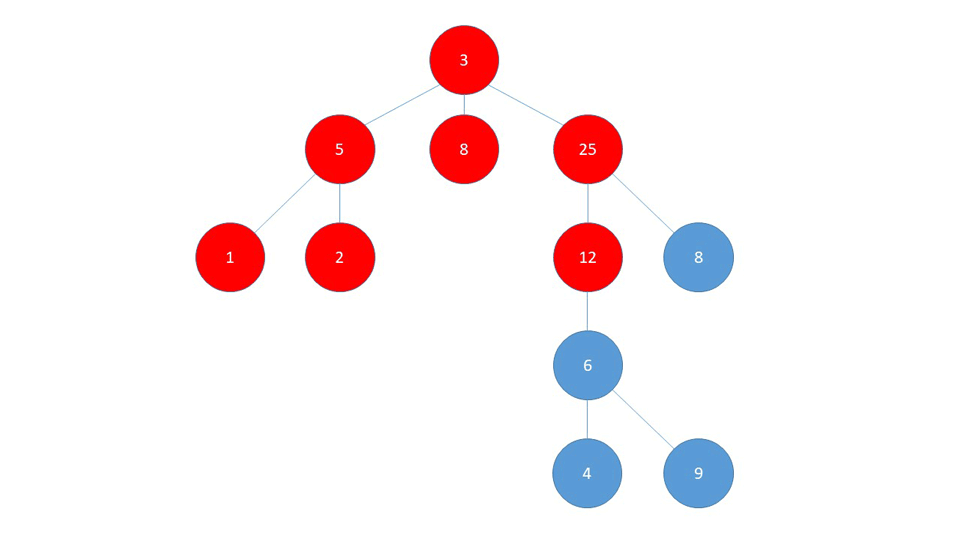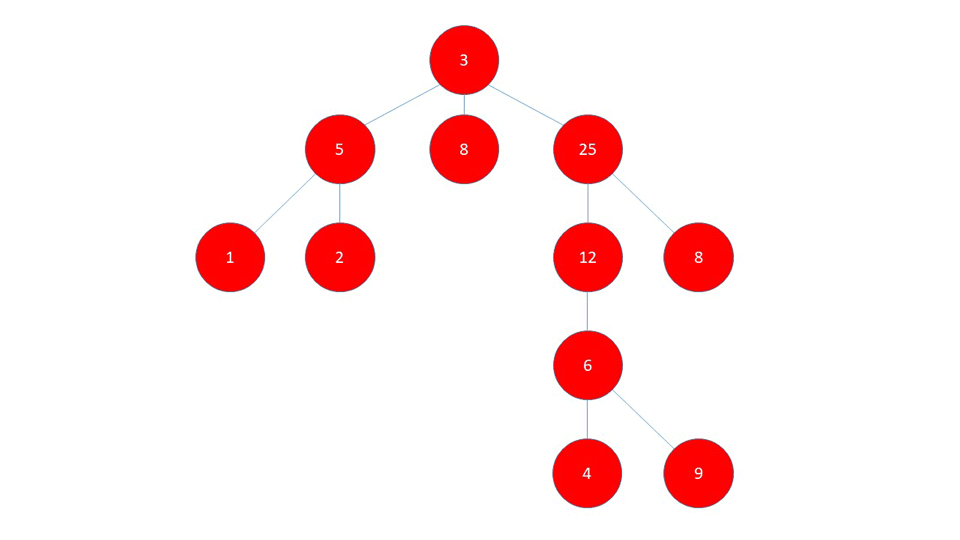
Definition
A Graph data structure consists of a finite (and possibly mutable) set of vertices or nodes or points, together with a set of unordered pairs of these vertices for an undirected Graph or a set of ordered pairs for a directed Graph. These pairs are known as edges, arcs, or lines for an undirected Graph and as arrows, directed edges, directed arcs, or directed lines for a directed Graph. The vertices may be part of the Graph structure, or may be external entities represented by integer indices or references. From Wikipedia
A Graph data structure may also associate to each edge some edge value, such as a symbolic label or a numeric attribute (cost, capacity, length, etc.).
Representation There are different ways of representing a graph, each of them with its own advantages and disadvantages. Here are the main 2:
Adjacency list: For every vertex a list of adjacent vertices is stored. This can be viewed as storing the list of edges. This data structure allows the storage of additional data on the vertices and edges. Adjacency matrix: Data are stored in a two-dimensional matrix, in which the rows represent source vertices and columns represent destination vertices. The data on the edges and vertices must be stored externally. Complexity Adjacency list Storage Add Vertex Add Edge Query O( V + E Adjacency matrix Storage Add Vertex Add Edge Query O( V ^2) O(
Graph
The code
//below uses the adjacency list representation.
function Graph() {
this.vertices = [];
this.edges = [];
this.numberOfEdges = 0;
}
Graph.prototype.addVertex = function(vertex) {
this.vertices.push(vertex);
this.edges[vertex] = [];
};
Graph.prototype.removeVertex = function(vertex) {
let index = this.vertices.indexOf(vertex);
if(~index) {
this.vertices.splice(index, 1);
}
while(this.edges[vertex].length) {
let adjacentVertex = this.edges[vertex].pop();
this.removeEdge(adjacentVertex, vertex);
}
};
Graph.prototype.addEdge = function(vertex1, vertex2) {
this.edges[vertex1].push(vertex2);
this.edges[vertex2].push(vertex1);
this.numberOfEdges++;
};
Graph.prototype.removeEdge = function(vertex1, vertex2) {
let index1 = this.edges[vertex1] ? this.edges[vertex1].indexOf(vertex2) : -1;
let index2 = this.edges[vertex2] ? this.edges[vertex2].indexOf(vertex1) : -1;
if(~index1) {
this.edges[vertex1].splice(index1, 1);
this.numberOfEdges--;
}
if(~index2) {
this.edges[vertex2].splice(index2, 1);
}
};
Graph.prototype.size = function() {
return this.vertices.length;
};
Graph.prototype.relations = function() {
return this.numberOfEdges;
};
Graph.prototype.traverseDFS = function(vertex, fn) {
if(!~this.vertices.indexOf(vertex)) {
return console.log('Vertex not found');
}
let visited = [];
this._traverseDFS(vertex, visited, fn);
};
Graph.prototype._traverseDFS = function(vertex, visited, fn) {
visited[vertex] = true;
if(this.edges[vertex] !== undefined) {
fn(vertex);
}
for(let i = 0; i < this.edges[vertex].length; i++) {
if(!visited[this.edges[vertex][i]]) {
this._traverseDFS(this.edges[vertex][i], visited, fn);
}
}
};
Graph.prototype.traverseBFS = function(vertex, fn) {
if(!~this.vertices.indexOf(vertex)) {
return console.log('Vertex not found');
}
let queue = [];
queue.push(vertex);
let visited = [];
visited[vertex] = true;
while(queue.length) {
vertex = queue.shift();
fn(vertex);
for(let i = 0; i < this.edges[vertex].length; i++) {
if(!visited[this.edges[vertex][i]]) {
visited[this.edges[vertex][i]] = true;
queue.push(this.edges[vertex][i]);
}
}
}
};
Graph.prototype.pathFromTo = function(vertexSource, vertexDestination) {
if(!~this.vertices.indexOf(vertexSource)) {
return console.log('Vertex not found');
}
let queue = [];
queue.push(vertexSource);
let visited = [];
visited[vertexSource] = true;
let paths = [];
while(queue.length) {
let vertex = queue.shift();
for(let i = 0; i < this.edges[vertex].length; i++) {
if(!visited[this.edges[vertex][i]]) {
visited[this.edges[vertex][i]] = true;
queue.push(this.edges[vertex][i]);
// save paths between vertices
paths[this.edges[vertex][i]] = vertex;
}
}
}
if(!visited[vertexDestination]) {
return undefined;
}
let path = [];
for(let j = vertexDestination; j != vertexSource; j = paths[j]) {
path.push(j);
}
path.push(j);
return path.reverse().join('-');
};
Graph.prototype.print = function() {
console.log(this.vertices.map(function(vertex) {
return (vertex + ' -> ' + this.edges[vertex].join(', ')).trim();
}, this).join(' | '));
};
```
let graph = new Graph();
graph.addVertex(1);
graph.addVertex(2);
graph.addVertex(3);
graph.addVertex(4);
graph.addVertex(5);
graph.addVertex(6);
graph.print(); // 1 -> | 2 -> | 3 -> | 4 -> | 5 -> | 6 ->
graph.addEdge(1, 2);
graph.addEdge(1, 5);
graph.addEdge(2, 3);
graph.addEdge(2, 5);
graph.addEdge(3, 4);
graph.addEdge(4, 5);
graph.addEdge(4, 6);
graph.print(); // 1 -> 2, 5 | 2 -> 1, 3, 5 | 3 -> 2, 4 | 4 -> 3, 5, 6 | 5 -> 1, 2, 4 | 6 -> 4
console.log('graph size (number of vertices):', graph.size()); // => 6
console.log('graph relations (number of edges):', graph.relations()); // => 7
graph.traverseDFS(1, function(vertex) { console.log(vertex); }); // => 1 2 3 4 5 6
console.log('---');
graph.traverseBFS(1, function(vertex) { console.log(vertex); }); // => 1 2 5 3 4 6
graph.traverseDFS(0, function(vertex) { console.log(vertex); }); // => 'Vertex not found'
graph.traverseBFS(0, function(vertex) { console.log(vertex); }); // => 'Vertex not found'
console.log('path from 6 to 1:', graph.pathFromTo(6, 1)); // => 6-4-5-1
console.log('path from 3 to 5:', graph.pathFromTo(3, 5)); // => 3-2-5
graph.removeEdge(1, 2);
graph.removeEdge(4, 5);
graph.removeEdge(10, 11);
console.log('graph relations (number of edges):', graph.relations()); // => 5
console.log('path from 6 to 1:', graph.pathFromTo(6, 1)); // => 6-4-3-2-5-1
graph.addEdge(1, 2);
graph.addEdge(4, 5);
console.log('graph relations (number of edges):', graph.relations()); // => 7
console.log('path from 6 to 1:', graph.pathFromTo(6, 1)); // => 6-4-5-1
graph.removeVertex(5);
console.log('graph size (number of vertices):', graph.size()); // => 5
console.log('graph relations (number of edges):', graph.relations()); // => 4
console.log('path from 6 to 1:', graph.pathFromTo(6, 1)); // => 6-4-3-2-1